This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Sam Bowyer, Equal contribution, Department of Mathematics and sam.bowyer@bristol.ac.uk;
(2) Thomas Heap, Equal contribution, Department of Computer Science University of Bristol and thomas.heap@bristol.ac.uk;
(3) Laurence Aitchison, Department of Computer Science University of Bristol and laurence.aitchison@bristol.ac.uk.
Table of Links
- Abstract & Introduction
- Related work
- Background
- Methods
- Experiments
- "Conclusion, Limitations, and References"
- Derivations
- Algorithms
- Experimental Datasets And Model
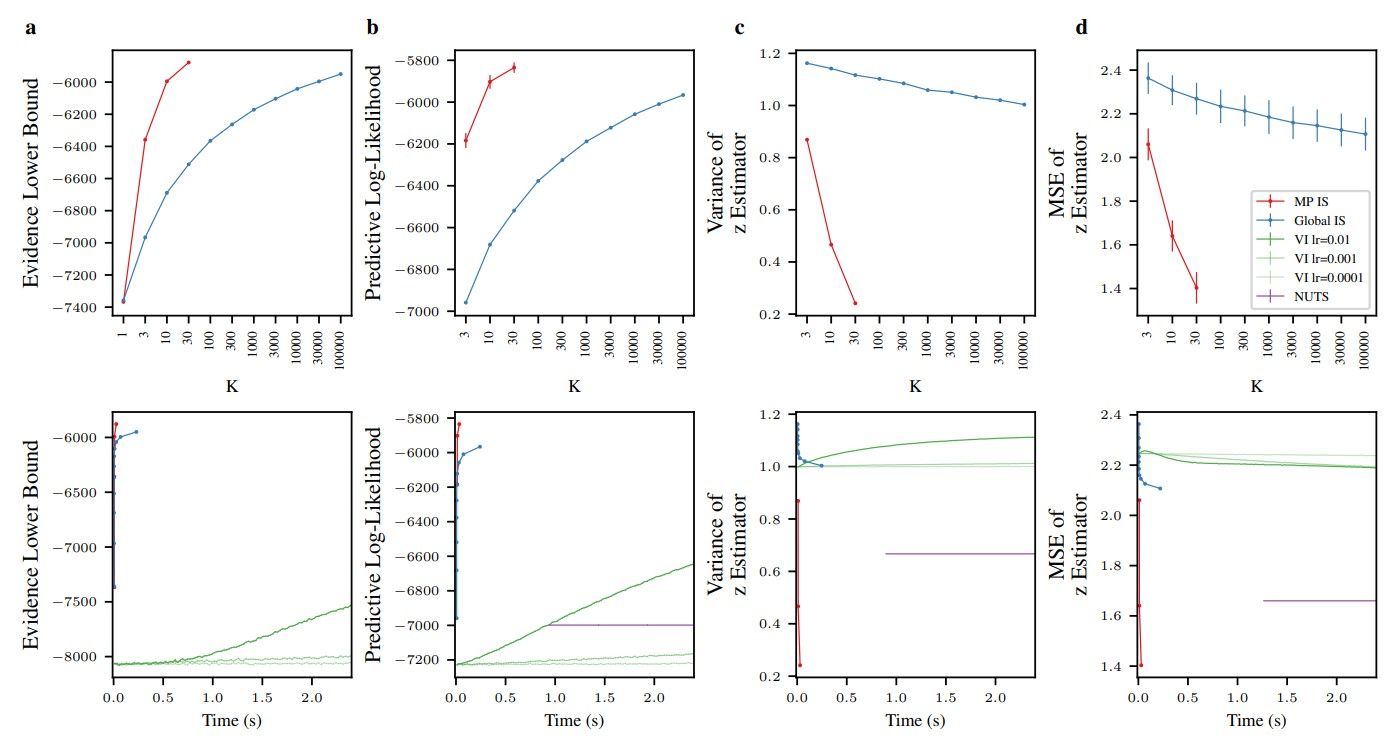
Methods
Of course, the contributions of this paper are not in computing the unbiased marginal likelihood estimator, which previously has been used in learning general probabilistic models, but instead our major contribution is a novel approach to computing key quantities of interest in Bayesian computation by applying the source term trick to the massively parallel marginal likelihood estimator. In particular, in the following sections, we outline in turn how to compute posterior expectations, marginals and samples.
