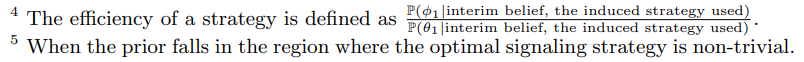Authors:
(1) Shih-Tang Su, University of Michigan, Ann Arbor ([email protected]);
(2) Vijay G. Subramanian, University of Michigan, Ann Arbor and ([email protected]);
(3) Grant Schoenebeck, University of Michigan, Ann Arbor ([email protected]).
Table of Links
2.1 Model of Binary-Outcome Experiments in Two-Phase Trials
3 Binary-outcome Experiments in Two-phase Trials and 3.1 Experiments with screenings
3.2 Assumptions and induced strategies
3.3 Constraints given by phase-II experiments
3.4 Persuasion ratio and the optimal signaling structure
3.5 Comparison with classical Bayesian persuasion strategies
4.2 Determined versus sender-designed experiments
4.3 Multi-phase model and classical Bayesian persuasion and References
3.3 Constraints given by phase-II experiments
By her choice of the experiment in phase I, the sender decides how to split the prior into the interim beliefs for the two experiments available in phase-II. The resulting interim-beliefs then lead to certain induced strategies at stage-II being applicable, i.e., incentive compatible (for the receiver). In other words, the probability pair (p1, p2) must make each (applied) induced strategy yield the maximum utility for the receiver. These requirements constrain the sender’s choice of (p1, p2), and the sender needs to account for the (reduced) choice while deciding the split of the prior. Table 1 summarizes the impact in terms of the parameters of the phase-I experiment via primary requirements on (p1, p2) driven by the incentive compatibility while using each class of induced strategies. Hereafter, when we use IC requirements without additional specification, we mean primary IC requirements. From the entries in the table, it is clear that the phase-II experiments (indirectly) limit the sender’s strategy selection where this limitation arises due the receiver’s IC requirements for each induced strategy (when that induced strategy is used).
With this in mind, the sender’s experiment design in phase I, essentially, is to select between different combinations of these induced strategies such that each induced strategy satisfies the constraint listed in Table 1. Hence, we next seek to understand how these IC constraints collectively determine the sender’s strategy selection. To answer this, we first discuss the relationship between induced strategies, IC requirements, and the sender’s expected utility.


taken, she would like to use the “most efficient”[4] pair of induced strategies to persuade the receiver[5]. To better understand the “efficiency” of induced strategies, we evaluate each induced strategy under a given phase-II experiment EX:




This paper is available on arxiv under CC 4.0 license.